Hallar recta tangente a una parábola

El siguiente ejercicio nos permitirá profundizar sobre las tangentes a una curva.

Si f(x) = x² + 6x + 11 y g(x) = -8x + b ¿cuánto debe valer b para que la recta sea tangente a la parábola?

Para empezar recordemos que:

Una recta tangente es aquella que solo tiene un punto en común con una curva, es decir la toca en un solo punto, que se llama punto de tangencia. La recta tangente indica la pendiente de la curva en el punto de tangencia.

Por lo tanto el punto de tangencia es un punto de la recta como de la parábola, por lo tanto en el punto de tangencia se cumple que:

f(x) = g(x)

x² + 6x + 11 = -8x + b

Simplificando y pasando todo a la izquierda tendremos:

x² + 6x + 11 + 8x – b = 0

x² + 14x + (11 – b) = 0       …I

Recordemos también que el discriminante de la ecuación cuadrática A x² + B x + C = 0, se define como:

∆ = B² – (4)(A)(C) ... II

En nuestra ecuación I

A = 1
B = 14
C = 11 - b

Para que el punto sea una tangente a la curva, el discriminante de esta ecuación tiene que ser cero.

Reemplazando valores en II, tendremos:

(14)² – (4)(1)(11 – b) = 0

196 – 44 + (4)(b) = 0

152 + (4)(b) = 0

(4)(b) = - 152

b = - 38

Por lo tanto la ecuación de la recta tangente a la parábola dada será:

g(x) = -8x – 38

El punto de tangencia lo hallaremos resolviendo la ecuación I

x² + 14x + (11 – b) = 0

x² + 14x + (11 + 38) = 0

x² + 14x + 49 = 0

(x + 7) ² = 0

De aquí:

x = - 7

Finalmente:

g(x) = -8x – 38

y = (- 8)(-7) – 38

y = 56 – 38

y = 18

El punto de tangencia será:

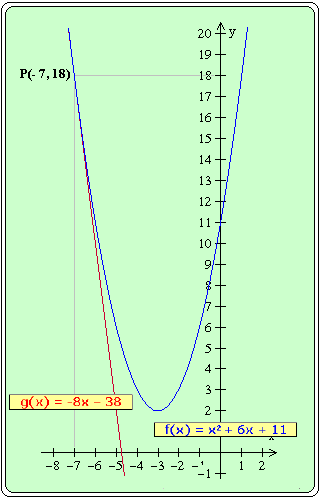
P(- 7, 18)

Y el gráfico de dichas funciones será el siguiente:

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Cometer un error y no corregirlo es otro error.

CONFUCIO