Aquí tienen otro ejercicio sobre geometría analítica similar al ejercicio anterior.
¿Halla la ecuación de la recta tangente a la circunferencia (x - 5)2 + (y - 3)2 = 5 en el punto E(7;2) de la misma?
Como sabemos la ecuación ordinaria de la circunferencia esta dada por la siguiente relación:
(x – h)2 + (y – k)2 = r2
|
Donde:
C(h;k) es el centro de la circunferencia
r es el radio de la circunferencia
P(x;y) es un punto genérico de la circunferencia.
De la ecuación de la circunferencia podemos deducir:
C(5,3) <=== Centro de circunferencia
r = √5 <=== Radio de circunferencia
Para resolver nuestro ejercicio, empezaremos hallando el valor de la pendiente de la recta que pasa por el punto E(7;2) y el centro de la circunferencia C(5;3):
m = (2 - 3)/(7 - 5)
m = -1/2
Por otro lado sabemos que para que dos rectas sean perpendiculares se debe cumplir que sus pendientes cumplan la siguiente relación:
(m)(m1) = -1
También sabemos que la recta tangente es perpendicular a la recta que pasa por el centro de la circunferencia y el punto de tangencia, por lo tanto:
m1 = (-1)/(m)
m1 = (-1)/(-1/2)
m1 = 2
Con este valor, ahora ya podemos definir la ecuación de la recta tangente:
2 = (y – 2)/(x-7)
(2)(x-7) = (y – 2)
Realizando operaciones tendremos la ecuación de la recta tangente:
y=2x-12
|
El gráfico de nuestra solución quedará de la siguiente manera:
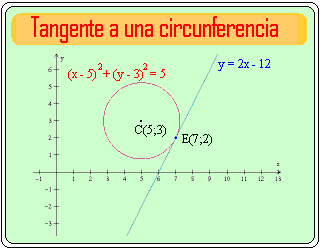
Si tuvieran alguna consulta adicional u otro ejercicio en el que necesiten ayuda, mi e-mail es jwzq2005@gmail.com con gusto los atenderé.
Tres clases hay de ignorancia: no saber lo que debiera saberse, saber mal lo que se sabe, y saber lo que no debiera saberse.

