Hallar recta tangente a una parábola

El siguiente ejercicio nos permitirá profundizar sobre las tangentes a una curva.

Si f(x) = x² + 6x + 11 y g(x) = -8x + b ¿cuánto debe valer b para que la recta sea tangente a la parábola?

Para empezar recordemos que:

Una recta tangente es aquella que solo tiene un punto en común con una curva, es decir la toca en un solo punto, que se llama punto de tangencia. La recta tangente indica la pendiente de la curva en el punto de tangencia.

Por lo tanto el punto de tangencia es un punto de la recta como de la parábola, por lo tanto en el punto de tangencia se cumple que:

f(x) = g(x)

x² + 6x + 11 = -8x + b

Simplificando y pasando todo a la izquierda tendremos:

x² + 6x + 11 + 8x – b = 0

x² + 14x + (11 – b) = 0       …I

Recordemos también que el discriminante de la ecuación cuadrática A x² + B x + C = 0, se define como:

∆ = B² – (4)(A)(C) ... II

En nuestra ecuación I

A = 1
B = 14
C = 11 - b

Para que el punto sea una tangente a la curva, el discriminante de esta ecuación tiene que ser cero.

Reemplazando valores en II, tendremos:

(14)² – (4)(1)(11 – b) = 0

196 – 44 + (4)(b) = 0

152 + (4)(b) = 0

(4)(b) = - 152

b = - 38

Por lo tanto la ecuación de la recta tangente a la parábola dada será:

g(x) = -8x – 38

El punto de tangencia lo hallaremos resolviendo la ecuación I

x² + 14x + (11 – b) = 0

x² + 14x + (11 + 38) = 0

x² + 14x + 49 = 0

(x + 7) ² = 0

De aquí:

x = - 7

Finalmente:

g(x) = -8x – 38

y = (- 8)(-7) – 38

y = 56 – 38

y = 18

El punto de tangencia será:

P(- 7, 18)

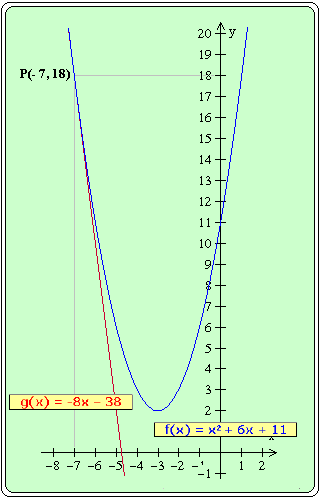
Y el gráfico de dichas funciones será el siguiente:

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Cometer un error y no corregirlo es otro error.

CONFUCIO

Soluciones - Número equivalente gramo

A continuación profundizamos un poco más nuestro conocimiento sobre soluciones.

Calcule el número de equivalentes en gramo y el peso en gramo del soluto que hay en 500 ml de una solución 0.4 normal de H₂SO₄.

El H₂SO₄ es un acido que tiene como carga iónica -2 ya que al disociarse queda como:

H₂SO₄ ===> 2H⁺ + SO₄^-2

La masa molecular del ácido sulfúrico (H₂SO₄) es:

2H = (2)(1) = 2 gr

S = (1)(32) = 32 gr

O = (4)(16) = 64 gr

La masa molecular de 1 mol de H₂SO₄ = 98 gr

Recordemos que se define un equivalente gramo de ácido como el peso en gramos de éste que puede producir un mol de H⁺.

Para calcular cuantos gramos le corresponden a 1 equivalente gramo de H₂SO₄ se divide:

Peso Molecular/Número de H⁺ producidos = 98 /2 = 49 gramos

El peso equivalente gramo del H₂SO₄ = 49 gr

La molaridad (M), o concentración molar, es el número de moles de soluto por cada litro de disolución.

Si la solución es 0.4 molar significa que hay 0.4 moles de soluto en 1000 cc (1 litro) de solución.

Como se desea calcular los datos en 500 cc

0.4 moles ---------------- 1000 cc

  n moles ----------------- 500 cc

n = 0.2 moles

Pero la masa molecular de 1 mol de H₂SO₄ = 98 gr

   1 mol     -------------- 98 gr

0.2 moles --------------- x gr

x = 19.6 gr

Por lo tanto:

masa molecular en 500 ml de H2SO4 0.4 M = 19.6 gr.

El número de equivalente gramo estará dado por

# eq-gr = Peso de la muestra / Peso equivalente de la sustancia

# eq-gr = 19.6 gr / 49 gr

# eq-gr en 500 ml de H2SO4 0.4 M = 0.4

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Es injusto que una generación sea comprometida por la precedente. Hay que encontrar un medio que preserve a las venideras de la avaricia o inhabilidad de las presentes.

NAPOLEÓN BONAPARTE

Neutralización - Equivalente gramo

El siguiente ejercicio nos permitirá profundizar sobre varios conceptos básicos que son importantes conocerlos.

¿Cuántos mililitros de NaOH 0,8 M se necesitan para neutralizar completamente la mezcla constituida por 20 ml de HCl 0,1 M y 10 ml de H₂SO₄ 0,1 M?

Recordemos algunas definiciones previas.

Una reacción de neutralización es una reacción entre un ácido y una base, con objeto de determinar la concentración de una sustancia ácida o básica en la disolución.

Cuando en la reacción participan un ácido fuerte y una base fuerte se obtiene una sal y agua. Generalmente la siguiente reacción ocurre:

ácido + base → sal + agua

Las reacciones de neutralización son generalmente exotérmicas, lo que significa que desprenden energía en forma de calor.

Equivalentes gramo de  ácidos y bases

Se define un equivalente gramo de ácido como el peso en gramos de éste que puede producir un mol de H⁺.

Se define un equivalente gramo de base como el peso en gramos de ésta que puede producir un mol de OH^–.

Por la misma naturaleza de las definiciones, un equivalente gramo de cualquier ácido puede neutralizar un equivalente gramo de cualquier base. En otras palabras:

# equivalentes gramo de ácido = # de equivalentes gramos de base

En la reacción de neutralización del ácido clorhídrico con el hidróxido de sodio:

HCl + NaOH à NaCl + H₂O

Un mol de HCl reacciona con un mol de NaOH. Podemos considerar esto como la reacción de un mol de H⁺ (del HCl) con un mol de OH^– (del NaOH). Por lo tanto, en lo que se refiere a la neutralización, lo que realmente nos interesa es que un mol de HCl neutraliza un mol de NaOH debido a la reacción entre un mol de H⁺ con un mol de OH^–. Esta última reacción tiene lugar cuando se juntan igual número de equivalentes gramo de ácido que de base.

En la reacción:

H₂SO₄ + 2NaOH à Na₂SO₄ + 2H₂O

Son necesarias dos moles de NaOH por mol de H₂SO₄, debido a que cada mol de H₂SO₄ proporciona dos moles de H⁺. Dos moles de NaOH son iguales a dos equivalentes gramo de base, por lo cual necesitamos 2 equivalentes gramo de ácido para la neutralización. Estos dos equivalentes gramo de ácido los proporciona el mol de H₂SO₄.

El único truco para averiguar los equivalentes gramo de un ácido o base, es saber qué cantidad de H⁺ o de OH^– puede proporcionar una molécula dada. En estos casos suponemos que se utiliza todo el  H⁺ disponible.

Es decir que para que exista neutralización se debe cumplir:

(# de cationes H+)(# moles de ácido) = (# de iones OH–)(# de moles de base)

Recordemos también que molaridad (M), o concentración molar, es el número de moles de soluto por cada litro de disolución. Por ejemplo, si se disuelven 0,5 moles de soluto en 1000 mL de disolución, se tiene una concentración de ese soluto de 0,5 M (0,5 molar).

# de moles de soluto = (molaridad)(volumen de disolución)

Finalmente para que exista neutralización se debe cumplir:

(# H+)(molaridad)(volumen de ácido)= (# OH–)(molaridad)(volumen de base)

(# H⁺)(M)(V)_HCL + (# H⁺)(M)(V) _H2SO4 = (#OH^–)(M)(V)_NaOH

(1)(0,1 M)(20 ml) + (2)(0,1 M)(10 ml) = (1)(0,8 M)(V _NaOH)

V _NaOH = 4/0,8

V NaOH = 5 ml

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Molaridad

El siguiente ejercicio nos servirá para recordar como utilizar la molaridad en las soluciones.

Calcule la densidad (en gr/ml) del ácido acético, CH₃COOH, al 99,8% en masa de soluto, cuya moralidad es 17,4.

Masa molar: CH₃COOH = 60

Recordemos algunos conceptos básicos previamente.

Una solución es una mezcla homogénea de dos o más sustancias. La sustancia disuelta se denomina soluto y esta presente generalmente en pequeña cantidad en comparación con la sustancia donde se disuelve denominada disolvente.

La molaridad (M), o concentración molar, es el número de moles de soluto por cada litro de disolución. Por ejemplo, si se disuelven 0,5 moles de soluto en 1000 mL de disolución, se tiene una concentración de ese soluto de 0,5 M (0,5 molar).

Por lo tanto:

Despejando la densidad:

ρ = (17,4)(6)/99,8

ρ = 1,046 gr/ml

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

No soy tan joven como para saberlo todo.

WILDE, Oscar Fingal O`Flahertie Wills

Enlace covalente

Empezaremos ahora a estudiar un poco de estequiometría. El siguiente ejercicio nos servirá para saber como determinar si un compuesto tiene enlace covalente o iónico.

En la siguiente serie de compuestos, seleccione al molécula de mayor carácter covalente:

MgCl₂

BaCl₂

SrCl₂

CaCl₂

BeCl₂

Datos:

Moléculas	Be	Mg	Ca	Ba	Sr	Cl
Numero atómico	4	12	20	56	36	17
electronegatividad	1,5	1,2	1,0	0,9	1,0	3,0

Empecemos recordando algunos conceptos previos importantes.

El carácter iónico-covalente de un enlace se puede analizar desde dos perspectivas: Electronegatividad y Polarización

El carácter covalente del enlace químico aparece al producirse la compartición de electrones entre los átomos enlazados. Esta compartición se da cuando la diferencia de electronegatividad entre los dos átomos enlazados no es muy grande, resultando muy desfavorable la energética de la formación de iones.

El carácter covalente de un enlace varía en forma inversa a la diferencia de electronegatividades.

Enlace covalente ---> aumenta ∆(EN) ---> enlace iónico A menor ∆(EN) ===> Mayor carácter covalente del enlace

Cuando la diferencia de electronegatividades es nula (es el caso de dos átomos iguales), el enlace formado será covalente; para una diferencia de electronegatividades de 1,7 el carácter iónico alcanza ya el 50%, y para una diferencia de 3, será del 95%.

Por lo tanto:

MgCl₂ ===> ∆(EN) = 3,0 – 1,2 = 1,8

BaCl₂ ===> ∆(EN) =  3,0 – 0,9 = 2,1

SrCl₂ ===> ∆(EN) = 3,0 – 1,0 = 2,0

CaCl₂ ===> ∆(EN) = 3,0 – 1, 0 = 2,0

BeCl₂ ===> ∆(EN) = 3,0 – 1,5 = 1,5

De aquí podemos observar que el compuesto con menor ∆(EN) y por lo tanto mayor carácter covalente del enlace es:

BeCl2

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Los jóvenes hoy en día son unos tiranos. Contradicen a sus padres, devoran su comida, y le faltan al respeto a sus maestros.

SÓCRATES

Comparación de movimiento parabólico y tiro vertical

El siguiente ejercicio nos permitirá analizar y comparar el movimiento compuesto con el tiro vertical. Espero que les agrade.

2. Si estoy parada en el borde de un risco y lanzo una piedra verticalmente hacia arriba con v_o=10m/s. antes de que golpee el piso tiene una rapidez de 30m/s. si fuera a lanzarla horizontalmente fuera del risco con la misma v_o de 10m/s ¿cuán rápido viajaría la piedra antes de golpear el piso?

Primero representemos mediante un gráfico nuestro ejercicio:

Por datos del ejercicio:

V_oy1 = 10 m/s

V_fy1 = 30 m/s

V_oy2 = 0 m/s   (Dado que no tiene componente vertical)

V_ox2 = V_fx2 =10 m/s ===> movimiento horizontal uniforme (MRU)

V_f2 = ¿? m/s

Podemos utilizar la siguiente fórmula para relacionar ambos movimientos:

(V_f)² = (V_o)²  + (2)(g)(h)

Para el primer movimiento:

(V_fy1)² = (V_oy1)²  + (2)(g)(h) ===> (2)(g)(h) = (V_fy1)² - (V_oy1)²

Para el segundo movimiento:

(V_fy2)² = (V_oy2)²  + (2)(g)(h) ===> (2)(g)(h) = (V_fy2)² - (V_oy2)²

Igualando ambas las ecuaciones obtenidas, tendremos:

(V_fy2)² - (V_oy2)² = (V_fy1)² - (V_oy1)²

(V_fy2)² = (V_fy1)² - (V_oy1)² + (V_oy2)²

Reemplazando valores:

(V_fy2)² = (30)² - (10)² + (0)²

(V_fy2)² = 800

Por Pitágoras sabemos que la rapidez en un movimiento parabólico está dado por:

(V_f2)² = (V_fx2)² + (V_fy2)²

Reemplazando valores:

(V_f2)² = (10)² + 800

(V_f2)² = 900

Vf2 = 30 m/s

Respuesta: la piedra antes de golpear el piso viajará con una rapidez de 30 m/s

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Nos gusta llamar testarudez a la perseverancia ajena pero le reservamos el nombre de perseverancia a nuestra testarudez.

KARR, Jean-Baptiste Alphonse

Término generico de una sucesión aritmética

El siguiente ejercicio nos ayudará a repasar como hallar el término genérico de una sucesión:

Hallar el término general de las siguientes sucesiones:

a). 3, 6, 12, 24, 48, ……….

b). 4, -9, 16, -25, 36, -49, ...

c). 2/4, 5/9, 8/16, 11/25, 14/36,...

Recordemos que se denomina sucesión a una función cuyo dominio es el conjunto de los números naturales.

a). 3, 6, 12, 24, 48, ……….

Aquí, podemos ver que

3 = 3 (1)

6 = 3 (2)

12 = 3 (2²)

24 = 3 (2³)

48 = 3 (2⁴)

Pero también debemos recordar que:

2⁰ = 1

2¹ = 2

Además sí: n = 1,2,3,4, 5, ...........

El término general buscado será:

tn = (3)(2)(n-1)

b). 4, -9, 16, -25, 36, -49, ...

Aquí podemos ver que:

4 = (1)(2²)

-9 = (-1)(3²)

16 = (1)(4²)

-25 =(-1)(5²)

36 = (1) (6²)

-49 = (-1)(7²)

Además sí: n = 1,2,3,4, 5, ...........

tenemos que para n número impar:

(-1)⁽ⁿ⁺¹⁾ = 1

para n número par:

(-1)⁽ⁿ⁺¹⁾ = -1

Por lo tanto el término general será:

tn = [(-1)(n+1)](n+1)2

c). 2/4, 5/9, 8/16, 11/25, 14/36,...

Analizaremos primero los numeradores:

2 = 2

5 = 2 + 3

8 = 2 + (3)(2)

11 = 2 + (3)(3)

14 = 2 + (3)(4)

Además sí: n = 1,2,3,4, 5, ...........

La relación para el numerador será:

2 + (3)(n – 1)

Analizaremos ahora el denominador:

4 = 2²

9 = 3²

16 = 4²

25 = 5²

36 = 6²

La relación para el denominador será:

(n + 1)2

Por lo tanto el término general será:

tn = [2 + (3)(n – 1)]/ (n + 1)2

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Es duro caer, pero es peor no haber intentado nunca subir.

ROOSEVELT, Theodore

Caida libre y tiro vertical

El siguiente ejercicio nos ayudará a comprender como se relaciona la caída libre y el tiro vertical.

 3. Una piedra es lanzada verticalmente hacia arriba desde el techo de un edificio con una velocidad de 29,4 m/s. Otra piedra se deja caer 4 segundos después de la primera. Demostrar que la piedra pasará a la segunda exactamente 4 segundos después.

Lo primero que debemos hacer nuestro diagrama de tiro vertical y caída libre sobre el cual trabajaremos

De acuerdo con el ejercicio los datos que tenemos son:

v_o1 = 29.4 m/s

v_o2 = 0 m/s

g = 9.8 m/s²

h = ? m

Cuando ambas piedras se encuentren a la misma altura o nivel, la primera piedra habrá estado en movimiento durante un intervalo de tiempo de (t + 4) segundos y la segunda piedra sólo un tiempo de t segundos.

t₁ = t + 4

t₂ = t

Igualando los desplazamientos de las piedras tendremos:

h₁ = h₂

Utilizaremos la siguiente fórmula para calcular la altura:

h = V_o t + (g/2)(t²)

De aquí:

V_o1 t₁ + (-g/2)(t₁²) = V_o2 t₂ + (-g/2)(t₂²)

Reemplazando valores:

(29.4)( t + 4) - (9.8/2)( t + 4)² = (0)( t) - (9.8/2)(t²)

29.4t + 117.6 - (4.9)(t² + 8t + 16) = - 4.9 t²

29.4t + 117.6 - 4.9 t² – 39.2t - 78.4 = - 4.9 t²

- 9.8t + 39.2 = 0

t = 4 s

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

El recuerdo que deja un libro es más importante que el libro mismo.

BÉCQUER, Gustavo Adolfo

Caida libre conociendo tiempo total

El siguiente ejercicio ya lo hemos desarrollado antes (ver: http://distribuyendoconocimiento.blogspot.com/2009/08/caida-libre-conociendo-tiempo-total.html), pero esta vez lo desarrollaremos utilizando las medidas en el sistema inglés, aprovechando una consulta que nos envían.

 5. Se deja caer una piedra desde lo alto de un edificio. El sonido de la piedra al chocar con el suelo se escucha 6,5 s más tarde. Si la velocidad (constante) del sonido es de 1120 pies/s, calcular la altura del edificio.

El siguiente es el diagrama de caída libre sobre el cual trabajaremos y donde ubicamos en el fondo del edificio el origen de coordenadas de nuestro sistema de referencia:

Por datos del ejercicio:

V_o = velocidad inicial de la piedra = 0 pies/s

V_s = velocidad del sonido = 1120 pies/s

t = Tiempo total= 6.5 s

g = aceleración de la gravedad a nivel del mar = 32.17 pies/s²

El siguiente cuadro muestra las fórmulas que rigen el tiro vertical y la caída libre

Lo que tenemos que saber para resolver este ejercicio es:

Por condición del ejercicio, el tiempo total de 6.5 s está formado por el tiempo que la piedra emplea en tocar el suelo más el que demora el sonido del impacto en llegar a la superficie, es decir:

t = t_p + t_s = 6.5 s

(i) t_s = 6.5 - t_p

También por condición del ejercicio, la distancia que recorre la piedra es igual a la distancia que recorre el sonido. Es decir:

(ii) h_s = h_p

Para hallar la altura   que recorre la piedra, cuya velocidad inicial es nula, utilizaremos la fórmula (4)

h_p = V_o t_p + (g/2)(t_p²)

Reemplazando valores:

h_p = (0) t_p +(32.17/2)(t_p²)

h_p = (32.17/2)(t_p²)

(iii) h_p = (16.085) t_p²

Dado que la velocidad del sonido es constante, en un medio ambiente determinado, utilizaremos la fórmula del M.R.U.

h_s = V_s.t_s

Pero de (ii) reemplazando valores:

h_p = (1120)t_s

De (i)

h_p = (1120)(6.5 - t_p)

(iv) h_p = 7280 – (1120) t_p

Igualando (iii) = (iv)

(16.085) t_p² = 7280 – (1120) t_p

(16.085) t_p² + (1120) t_p – 7280 = 0

La única solución posible para esta ecuación es:

t_p = 5.99 s

Para hallar la altura del pozo utilizaremos la fórmula (4)

h_p = v_o t_p + (g/2)(t_p²)

Reemplazando valores

h_p = (0)(5.99) + (32.17/2)(5.99)²

h_p = 577.13 pies

Respuesta: la altura del edificio es de 577.13 pies

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Si crees que la enseñanza es cara, prueba con la ignorancia.

Anónimo