-->
Empezamos ahora con el primer ejercicio sobre movimiento parabólico también conocido como movimiento compuesto. El enunciado es el siguiente:

-->
Lo primero que debemos hacer para desarrollar un ejercicio es graficarlo:

--> -->
El ejercicio nos da los siguientes datos:
Para hmax/2
vfhmax/2 = (3/4)(vo)……………(IV)
-->
Parecen muy pocos datos ¿no? Para averiguarlo primero revisemos las fórmulas que podemos aplicar al movimiento parabólico:
Utilicemos la fórmula (2) dado que tenemos las relaciones de todas las incógnitas:
(vf)2 = (voy)2 – 2× g× h
h = [(voy)2 – (vf)2]/(2× g)…………(I)
Pero recordemos que:
"Un cuerpo alcanza su altura máxima cuando su velocidad de ascenso se hace igual a cero"
vf = 0 m/s
Reemplazando en (I)
hmax = (voy)2/(2× g)
hmax/2 = (voy)2/(4× g)
Volvamos a escribir ahora la fórmula (2) pero para cuando h = hmax/2
(vfyhmax/2)2 = (voy)2 – 2× g× hmax/2
(vfyhmax/2)2 = (voy)2 – [2× g×(voy)2/(4× g)]
(vfyhmax/2)2 = (voy)2/2……………(II)
Debemos recordar que para el movimiento parabólico la velocidad :
vox = constante
Para hallar el valor de la velocidad final cuando h = hmax/2 utilizaremos el teorema de pitágoras:
(vfhmax/2)2 = (vox)2 + (vfyhmax/2)2………………(III)
Reemplazando (II) en (III)
(vfhmax/2)2 = (vox)2 + [(voy)2/2]………(V)
Reemplazando (IV) en (V)
(3/4)2(vo)2 = (vox)2 + [(voy)2/2]………….(VI)
Por pitágoras:
(vo)2 = (vox)2 + (voy)2……………(VII)
Reemplazando (VII) en (VI)
(3/4)2[(vox)2 + (voy)2]= (vox)2 + [(voy)2/2]
(voy)2 = (7) (vox)2

Recordemos que:
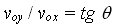
Por lo tanto:

Respuesta: El ángulo que forma el vector velocidad inicial con la horizontal es 69º 18’
-->
Espero que les sea de utilidad este desarrollo.
-->
Si tuvieran alguna consulta adicional u otro ejercicio en el que necesiten ayuda, mi e-mail es jwzq2005@gmail.com con gusto los atenderé.
"Una de las cosas más agradables de los problemas, es que muchos de ellos sólo existen en nuestra imaginación."
ALLEN, STEVE 1921 - 2000
-->



