El siguiente ejercicio nos acaba de llegar y como es uno parecido al que ya hemos solucionado, lo que haremos es encontrar una solución general.
¡Que lo disfruten!

Lo primero que debemos hacer para desarrollar un ejercicio es graficarlo:
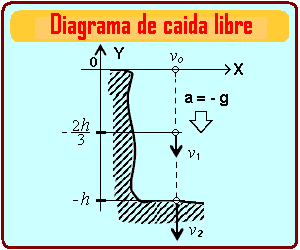
Hemos tomado nuestro sistema de referencia la parte alta del acantilado.
Los datos del ejercicio son:
h = altura del acantilado = ¿?
t1 =tiempo que tarda en recorrer (2h/3) = ¿?
t2 =tiempo que tarda en recorrer h/3 = 1 s
t = tiempo total = t1 + t2
g = aceleración de la gravedad = 9.8 m/s2
vo = velocidad en la cima del acantilado = 0 m/s (ya que se deja caer desde el reposo)
v1 = velocidad cuando ya ha recorrido (2/3) h
Como el tiro vertical y caída libre de un cuerpo es un movimiento rectilíneo uniformemente variado (MRUV), las fórmulas que se aplican serán las indicadas en la figura: 
Utilizaremos la fórmula (4) para deducir el tiempo y la fórmula (1) para relacionar las velocidades:
h = Vo•t + (g/2)•(t2)
Vf = Vo + (g)•t
Para el primer tramo tendremos:
–2h/3 = (0)•t + (– g/2)•(t12)
h = (3g/4)•(t12) …………..(I)
v1 = 0 – g•t1
v1 = – g•t1
Para el Segundo tramo tendremos:
–h/3 = v1•t2 – (g/2)•(t22)
h = – 3•v1•t2 + (3•g/2)•(t22)
Reemplazando el valor de v1
h = 3•g•t1•t2 + (3•g/2)•(t22)……………..(II)
Igualando (I) = (II)
(3•g/4)•(t12) = 3•g•t1•t2 + (3•g/2)•(t22)
Despejando tendremos:
t12 – 4•t1•t2 – (2)•(t22) = 0
La solución para esta ecuación es:

Reemplazando en la fórmula 4 tendremos:
h = Vo•t – (g/2)(t2)
h = (0)•t – (g/2)(t2)
Reemplazando valores:

h = – (145.51) t22
Por dato de nuestro ejercicio:
t2 = 1 s
h = – (145.51)•(1)2
h = – (145.51) m
Respuesta: El acantilado tiene una altura de 145.51 m
“No podemos resolver problemas pensando de la misma manera que cuando los creamos.”
Albert Einstein 1879 - 1955
No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

