86. Un hombre sobre un furgón plano que viaja con rapidez constante de 9,10 m/s, como se muestra en la figura P3.86, quiere lanzar una pelota a través de un aro estacionario a 4.90 m sobre la altura de la mano, de modo que la pelota se mueva horizontalmente al pasar por el aro. El hombre lanza la bola con una rapidez de 10.8 m/s respecto a si mismo.
a) ¿Qué componente vertical debe tener la velocidad inicial de la pelota?
b) ¿Cuántos segundos después del lanzamiento, la pelota atravesará el aro?
c) ¿A qué distancia horizontal del aro deberá soltar la pelota?
d) Cuando la pelota deja la mano del hombre, ¿qué dirección tiene su velocidad relativa al marco de referencia del furgón? ¿Relativa al marco de referencia de un observador parado en el suelo?
El movimiento siempre es un concepto relativo porque debe referirse a un sistema de referencia o referencial particular escogido por el observador.
En nuestro caso, el movimiento relativo hará referencia al que presenta la pelota con respecto a un sistema de referencia (x’ - y’), llamado referencial relativo o móvil (fijado en el hombre) por estar en movimiento con respecto a otro sistema de referencia (x - y) considerado como referencial absoluto o fijo (fijado en la tierra).
Grafiquemos nuestro ejercicio.
Denominemos:
P = pelota
H = hombre
T = tierra
Del enunciado de nuestro ejercicio tenemos los siguientes datos:
Donde:
voxP/H = voP/H cos θ
voyP/H = voP/H sen θ
voP/H = 10,8 m/s
|
θ es el ángulo medido respecto al hombre
Dado que el furgón viaja con rapidez constante, tendremos que:
axF/T = 0
dado que el furgón esta sostenido en los rieles y por lo tanto no esta cayendo:
ayF/T = 0
Como el hombre está sobre el furgón, entonces:
axH/T = axF/T = 0
ayH/T = ayF/T = 0
Además, la aceleración de la pelota respecto a la tierra es la aceleración de la gravedad (g), luego:
ayP/T = ayP/F = – 9,8 m/s2
Finalmente la aceleración vertical de la pelota respecto al hombre, se calcula mediante la siguiente expresión:
ayP/H = ayP/T – ayH/T
ayP/H = – 9,8 m/s2 – 0
ayP/H = – 9,8 m/s2
a) Como la aceleración vertical es constante, podemos analizar el movimiento vertical de la pelota mediante la siguiente ecuación:
(vfyP/H)2 = (voyP/H)2 + (2)(ayP/H)(yfyP/H – yoyP/H)
Cuando la pelota pase por el aro su movimiento es horizontal y por lo tanto se encuentra en su punto de altura máxima. Luego:
(0)2 = (voyP/H)2 + (2)( – 9,8)(4,90 – 0)
voyP/H = 9,8 m/s
|
b) Para hallar después de cuanto tiempo la pelota atravesará el aro lo haremos con el movimiento vertical, donde:
vfyP/H = voyP/H + (ayP/H)(t)
0 = 9,8 + (- 9,8)(t)
t = 1 s
|
c) La componente horizontal de la rapidez inicial respecto al hombre estará dada por:
(voP/H )2 = (voxP/H )2 + (voyP/H )2
(10,8 )2 = (voxP/H )2 + (9,8 )2
Simplificando tendremos:
voxP/H = 4,54 m/s
|
Como (axH/T = 0) en el movimiento horizontal de la pelota, respecto al hombre, entonces la distancia horizontal del aro a la que se deberá soltar la pelota será:
xfP/H = xoP/H + (voxP/H)(t)
xfP/H = 0 + (4,54)(1)
xfP/H =
|
d) La dirección que tiene la velocidad de la pelota cuando deja la mano del hombre, relativa al marco de referencia del furgón, será la misma que la relativa al marco de referencia del hombre, esto es:
tg θP/F = tg θP/H = (voyP/H) /( voxP/H)
tg θP/F = (9,8) /(4,54)
tg θP/F = 2,1586
θP/F = 65,14º
|
Para determinar el ángulo de lanzamiento respecto a la Tierra , primero debemos determinar la velocidad inicial de la pelota respecto a la tierra.
Por lo tanto el ángulo de lanzamiento según un observador en la tierra es:
tg θP/T = (voyP/T) /( voxP/T)
tg θP/T = (9,8) /(13,64)
tg θP/T = 0,7185
θP/T = 35,7º
|
No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com




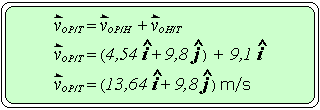

No hay comentarios:
Publicar un comentario