Semejanza de triángulos

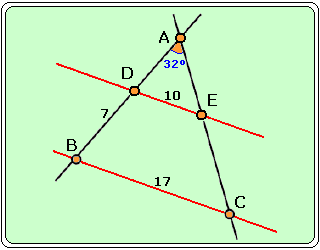
Las bases de un trapecio miden 17 cm y 10 cm, y uno de sus lados 7 cm. El ángulo que forman las rectas sobre las que se encuentran los lados no paralelos es de 32º. Calcula lo que mide el otro lado y el área del Trapecio.

Un trapecio es un cuadrilátero que tiene dos lados paralelos (las bases) y los otros dos no paralelos.

Para empezar grafiquemos nuestro ejercicio.

Sea BCED es el trapecio que nos dan, donde:

DE = 10cm

BC = 17cm

BD =7cm

EC = ¿?

La prolongación de los lados no paralelos BD y CE, se juntan en el punto A, por lo que:

BÂC = 32°.

1º Calculamos la medida del segmento AD.

Recordemos el teorema de Thales en un triángulo:

Dado un triángulo ABC, si se traza un segmento paralelo, DE, a uno de los lados del triangulo, se obtiene otro triángulo ADE, cuyos lados son proporcionales a los del triángulo ABC.

AD/DE=AB/BC

AD /10 = (AD +7)/17

(17)(AD) = (10)(AD) +70

(7)(AD) =70

AD = 10 cm

2º Calculamos la medida del segmento AE.

Recordemos el teorema del coseno:

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

En el triángulo ADE:

(DE)^² = (AD)^² + (AE)^² – (2)(AD)(AE)(cos32º)

(10)^² = (10)^² + (AE)^² – (2)(10)(AE)(0,848)

100 = 100 + (AE)^² – (16,96)(AE)

AE = 16,96 cm

3º Calculamos  la medida del segmento EC.

Volvemos a utilizar el teorema de Thales:

AD/DB = AE/EC

10/7 = 16,96/EC

EC = 11,87 cm

4º Calculamos el área del trapecio BCED.

Para calcular el área del trapecio, recordemos la llamada fórmula de Herón, que nos permite calcular el área de un triángulo conocidos los tres lados.

Si llamamos p al semiperímetro y a, b, c a los tres lados:

El área del trapecio estará dado por:

A_BCED = A_ABC – A_ADE

A_BCED = 129,90 – 44.94

ABCED = 84,96 cm2

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Movimiento compuesto

86. Un hombre sobre un furgón plano que viaja con rapidez constante de 9,10 m/s, como se muestra en la figura P3.86, quiere lanzar una pelota a través de un aro estacionario a 4.90 m sobre la altura de la mano, de modo que la pelota se mueva horizontalmente al pasar por el aro. El hombre lanza la bola con una rapidez de 10.8 m/s respecto a si mismo.

a)    ¿Qué componente vertical debe tener la velocidad inicial de la pelota?

b)     ¿Cuántos segundos después del lanzamiento, la pelota atravesará el aro?

c)    ¿A qué distancia horizontal del aro deberá soltar la pelota?

d)    Cuando la pelota deja la mano del hombre, ¿qué dirección tiene su velocidad relativa al marco de referencia del furgón? ¿Relativa al marco de referencia de un observador parado en el suelo?

El movimiento siempre es un concepto relativo porque debe referirse a un sistema de referencia o referencial particular escogido por el observador.

En nuestro caso, el movimiento relativo hará referencia al que presenta la pelota con respecto a un sistema de referencia (x’ - y’), llamado referencial relativo o móvil (fijado en el hombre) por estar en movimiento con respecto a otro sistema de referencia (x - y) considerado como referencial absoluto o fijo (fijado en la tierra).

Grafiquemos nuestro ejercicio.

Denominemos:

P = pelota

H = hombre

T = tierra

Del enunciado de nuestro ejercicio tenemos los siguientes datos:

Donde:

v_oxP/H  = v_oP/H  cos θ

v_oyP/H  = v_oP/H  sen θ

voP/H  = 10,8 m/s

θ es el ángulo medido respecto al hombre

Dado que el furgón viaja con rapidez constante, tendremos que:

a_xF/T = 0

dado que el furgón esta sostenido en los rieles y por lo tanto no esta cayendo:

a_yF/T = 0

Como el hombre está sobre el furgón, entonces:

a_xH/T = a_xF/T = 0

a_yH/T = a_yF/T = 0

Además, la aceleración de la pelota respecto a la tierra es la aceleración de la gravedad (g), luego:

a_yP/T = a_yP/F = – 9,8 m/s²

Finalmente la aceleración vertical de la pelota respecto al hombre, se calcula mediante la siguiente expresión:

a_yP/H = a_yP/T – a_yH/T

a_yP/H = – 9,8 m/s² – 0

a_yP/H = – 9,8 m/s²

a)     Como la aceleración vertical es constante, podemos analizar el movimiento vertical de la pelota mediante la siguiente ecuación:

(v_fyP/H)² = (v_oyP/H)² + (2)(a_yP/H)(y_fyP/H  – y_oyP/H)

Cuando la pelota pase por el aro su movimiento es horizontal y por lo tanto se encuentra en su punto de altura máxima. Luego:

(0)² = (v_oyP/H)² + (2)( – 9,8)(4,90  – 0)

voyP/H = 9,8 m/s

b)     Para hallar después de cuanto tiempo la pelota atravesará el aro lo haremos con el movimiento vertical, donde:

v_fyP/H = v_oyP/H + (a_yP/H)(t)

0 = 9,8 + (- 9,8)(t)

t = 1 s

c)     La componente horizontal de la rapidez inicial respecto al hombre estará dada por:

(v_oP/H )² = (v_oxP/H )² + (v_oyP/H )²

(10,8 )² = (v_oxP/H )² + (9,8 )²

Simplificando tendremos:

voxP/H  =  4,54 m/s

Como (a_xH/T = 0) en el movimiento horizontal de la pelota, respecto al hombre, entonces la distancia horizontal del aro a la que se deberá soltar la pelota será:

x_fP/H = x_oP/H + (v_oxP/H)(t)

x_fP/H = 0 + (4,54)(1)

xfP/H = 4,54 m

d)     La dirección que tiene la velocidad de la pelota cuando deja la mano del hombre, relativa al marco de referencia del furgón, será la misma que la relativa al marco de referencia del hombre, esto es:

tg θ_P/F = tg θ_P/H = (v_oyP/H) /( v_oxP/H)

tg θ_P/F = (9,8) /(4,54)

tg θ_P/F = 2,1586

θP/F = 65,14º

Para determinar el ángulo de lanzamiento respecto a la Tierra, primero debemos determinar la velocidad inicial de la pelota respecto a la tierra.

Por lo tanto el ángulo de lanzamiento según un observador en la tierra es:

tg θ_P/T = (v_oyP/T) /( v_oxP/T)

tg θ_P/T = (9,8) /(13,64)

tg θ_P/T = 0,7185

θP/T = 35,7º

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Movimiento compuesto

2005-1

Desde el punto P se lanza una pelota con una velocidad inicial de 50 m/s y dirigida paralela al plano z – y. Además sopla un viento perpendicular a ese plano que le comunica a la pelota una velocidad constante de 10 m/s en sentido negativo al eje x. Los puntos A y B se encuentran a la misma altura y se sabe que después de lanzada la pelota, esta ha pasado por dichos puntos. (considere g = 10 m/s).

a)    ¿Qué tiempo tarda la pelota en pasar por el punto B, desde que fue lanzada?

b)    ¿Cuáles son las coordenadas del punto A?

c)     ¿Cuáles son las coordenadas del punto B?

Por dato del ejercicio:

yB = 210 m

Las componentes de la velocidad inicial serán:

v_ox = - 10 m/s

v_oy = (v_o)(cos 53º) = (50 m/s)(3/5)

v_oy = 30 m/s

v_oz = (v_o)(sen 53º) =(50 m/s)(4/5)

v_oz = 40 m/s

En el plano x – y no interviene la aceleración de la gravedad por lo que el movimiento es MRU.

a)     Para calcular el tiempo que demora la pelota en pasar por el punto B usaremos los datos del eje y:

v_oy = d /t_PB    ==>    t_PB = d/ v_oy

t_PB = 210/30

tPB = 7 s

b)     Dado que se sabe que después de lanzada la pelota, esta ha pasado por los puntos A y B, esto quiere decir que estos puntos deben estar en la dirección de la resultante de las velocidades del plano x - y.  Esta rapidez estará dada por:

(v_oxy)² = (v_ox)² + (v_oy)²

(v_oxy)² = (30)² + (-10)²

(v_oxy)² = 1000

v_oxy = 31,623 m/s

Grafiquemos ahora como queda nuestro ejercicio:

Ahora, la altura de B estará dada por:

h_B = (v_oz)(t_PB) – (1/2)(g)(t_PB)²

h_B = (40)(7) – (10/2)(7)²

h_B = 280 - 245

h_B = z_B =35 m

zB =35 m

Pero:

h_B = h_A = z_A = 35 m

zA = 35 m

Con esto podemos determinar el tiempo que demora para pasar por A:

h_A = (v_oz)(t_PA) – (1/2)(g)(t_PA)²

35 = (40)(t_PA) – (10/2)(t_PA)²

Simplificando tendremos:

(t_PA)² – (8)( t_PA) + 7 = 0

 Resolviendo, obtenemos:

t_PA = 1 s

Con este dato procedemos a hallar las coordenadas en el plano x – y del punto A.

xA = 0 m

y_A = (v_oy)(t_PA)

y_A = (30)(1)

yA = 30 m

Las coordenadas del punto A son:

A(0, 30, 35)

La coordenada que falta del punto B será:

x_B = x_o + (v_ox)(t_PB)

x_B = 10 + (-10)(7)

xB = - 60 m

Las coordenadas del punto B son:

B(-60, 210, 35)

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Movimiento compuesto

62. Una persona de pie en lo alto de una roca semiesférica de radio R, patea una pelota (inicialmente en reposo en lo alto de la roca) para darle velocidad horizontal v_i como se ve en la figura P4.62. (a) ¿Cuál debe ser su rapidez inicial mínima si la pelota nunca debe tocar la roca después de ser pateada? (b) Con esta rapidez inicial, ¿a qué distancia de la base de la roca llega la pelota al suelo?

Volvamos a dibujar el gráfico que nos dan:

Recordemos que el movimiento parabólico se produce como consecuencia de dos movimientos:

a)     Un movimiento horizontal uniforme MRU

b)     Un movimiento vertical de caída libre MRUV

(a) Tomaremos nuestro nivel de referencia a nivel del suelo, por lo que la altura de la pelota y será:

Del gráfico podemos observar que para que la pelota no vuelva a tocar la roca, en todo momento se debe cumplir la siguiente inecuación:

x² + y² > R²

Reemplazando el valor de y:

(b)

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Movimiento compuesto

54.  Un jugador de baloncesto que mide 2,00 m de estatura está de pie sobre el piso, a 10,0 m de la canasta, como se ve en la figura P4.54, Si lanza el balón a un ángulo de 40,0º con la horizontal, ¿a qué rapidez inicial debe lanzarlo para que pase por el anillo sin tocar el tablero? La altura de la canasta es 3,05 m.

Recordemos que el movimiento parabólico se produce como consecuencia de dos movimientos:

a)     Un movimiento horizontal uniforme MRU

b)     Un movimiento vertical de caída libre MRUV

La posición de la pelota en función del tiempo es

d_x = (v_o•cosθ)•t

h_y =(v_o•senθ)•t - ½ g•t²

Donde:

d_x = desplazamiento horizontal de la pelota = 10,0 m

v_o = velocidad inicial de la pelota

t = tiempo del desplazamiento de la pelota

h_y = desplazamiento vertical de la pelota = 3,05 m – 2,00 m = 1,05 m

g = aceleración de la gravedad = 9.8 m/s²

θ = ángulo formado por el eje de las abscisas y el vector V_o = 40º

Sabemos que el alcance esta definido por:

d_x = (v_o•cosθ)•t

10,0 = (v_o)(cos 40,0º)(t)

t = (10,0) / (vo)(0,766)

El desplazamiento vertical de la pelota está dado por la fórmula:

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Movimiento compuesto

55. Cuando los jugadores de béisbol lanzan la pelota desde la parte lejana al bateador, por lo general la tiran para que rebote una vez antes de llegar al diamante, con la idea de que la pelota llega más pronto de esta forma. Suponga que el ángulo al cual una pelota que rebota sale del terreno, es el mismo que el ángulo al cual el jardinero la lanzó, como en la figura P4.55, pero que la rapidez de la pelota después del rebote es la mitad de la que era antes del rebote. (a) Si se supone que la pelota siempre es lanzada con la misma rapidez inicial, ¿a qué ángulo θ debe lanzar el jardinero la pelota para que recorra la misma distancia D con un rebote (trayectoria azul) que cuando lanza la pelota hacia arriba a 45,0º sin rebotar (trayectoria verde)? (b) Determinar la razón entre los tiempos para los tiros de un rebote y sin rebote.

Las condiciones especiales del ejercicio nos permiten poder usar la ecuación de alcance horizontal, la cual procederemos a deducir.

Dado que el tiempo para cualquier trayectoria parabólica simétrica esta dad por:

y_f = (v_yo)(t) – (g/2)(t)²

Si t = 0 en el nivel desde donde se lanza la pelota entonces el tiempo en que la pelota regresa al mismo nivel desde donde fue lanzado estará dado por:

0 = (v_o)(sen θ)(t) – (g/2)(t)²

(v_o)(sen θ)(t) = (g/2)(t)²

t = (2)(vo)(sen θ)/g

Pero sabemos que el alcance esta definido por:

d = (v_xo)(t)

d = (v_o)(cos θ)(t)

Reemplazando t:

d = (v_o)(cos θ)(2)(v_o)(sen θ) / g

d = (2)(v_o)²(cos θ)(sen θ) / g

Sabemos que: sen 2θ = (2)(sen θ)(cos θ)

Finalmente:

d = (vo)2(sen 2θ) / g

a) Cuando se lanza la pelota hacia arriba a 45,0º sin rebotar (trayectoria verde), la distancia recorrida será:

D = d₄₅  = (v_o)²(sen 90º) / g

D = (v_o)² / g

Cuando se lanza la pelota hacia arriba a un ángulo θ con rebote (trayectoria azul), la distancia recorrida será:

a) Nos piden que ambas distancias sean iguales por lo que:

Despejando tendremos:

Sen 2θ = 4/5

2θ = 53,13º

θ = 26,57º

b) Cuando se lanza la pelota hacia arriba a 45,0º sin rebotar (trayectoria verde), el tiempo empleado será:

t = t₄₅  = (2)(v_o)(sen 45º)/g

t = t₄₅  = (1,414)(v_o)/g

Cuando se lanza la pelota hacia arriba a un ángulo θ con rebote (trayectoria azul), la distancia recorrida será:

t = t₁ + t₂  = [(2)(v_o)(sen 26,57º)/g] + [(2)(v_o/2)(sen 26,57º)/g]

t = t₁ + t₂  = (3)( sen 26,57º)(v_o)/g

t = t₁ + t₂  = (1,342)(v_o)/g

La razón entre los tiempos para los tiros de un rebote y sin rebote es:

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com

Descomposición vectorial

Hallar las componentes de un vector de 10 unidades según dos direcciones que forman un ángulo de 70º si el vector forma con una de ellas un ángulo de 40º.

Recordemos un poco de la teoría de descomposición de vectores:

De acuerdo con esta teoría grafiquemos nuestro ejercicio:

Del gráfico podemos ver que lo que nos piden es un cambio de base en R².

Consideremos nuestra nueva base en R² la cual sigue las direcciones que forman un ángulo de 70º, entonces debemos tomar vectores unitarios que cumplan lo siguiente:

Para simplificar las operaciones hacemos coincidir una de las direcciones de la nueva base con el eje x, por lo tanto el vector unitario en esa dirección de la nueva base será:

El vector unitario en la otra dirección de la nueva base es:

El vector de 10 unidades en el sistema cartesiano tendrá como componentes:

Para calcular las componentes en la base dada se tiene que cumplir:

(7,66 , 6,428) = (r) (1, 0) + (t) (0,342 , 0,9397) … I

(7,66 , 6,428) = (r , 0) + (0,342 t , 0,9397 t)

(7,66 , 6,428) = (r + 0,342 t , 0 + 0,9397 t)

Ahora procedemos ha hallar los valores de r y t

Para t:

6,428 = 0 + 0,9397 t

t = 6,84

Para r:

7,66 = r + 0,342 t

7,66 = r + (0,342)(6,84)

7,66 = r + 2.34

r = 5,32

Por lo tanto las componentes del vector en la base dada serán:

No se olviden de que si tienen alguna duda o desean hacer alguna consulta, pueden escribirnos a jwzq2005@gmail.com