Hoy día analizaremos un ejercicio sobre cinemática y rozamiento.

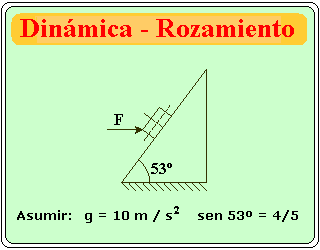
Para empezar dibujaremos nuestro diagrama de cuerpo libre:

El sistema coordenado se adapta al plano inclinado.
Se descompone el peso en sus dos componentes:
una en la dirección del plano inclinado (eje x):
Px = 50 sen 53º = (50)(4/5) = 40 N
y la otra, perpendicular a dicho plano (eje y):
Py = 50 cos 53º = (50)(3/5) = 30 N
Descomponemos también la fuerza F en sus dos componentes:
una en la dirección del plano inclinado (eje x):
Fx = 5k cos 53º = (5k)(3/5) = 3k N
y la otra, perpendicular a dicho plano (eje y):
Fy = 5k sen 53º = (5k)(4/5) = 4k N
La fuerza de fricción esta en el sentido contrario al movimiento del bloque y en la dirección del eje x:
f = µN
La reacción del plano inclinado hacia el bloque es una fuerza normal, perpendicular al plano.
Como el movimiento es uniforme, el bloque se encuentra en equilibrio cinético, por lo que se cumple que:
Σ F = 0
Σ Fx = 0 ==> 3k = 40 + f
3k = 40 + µN
3k = 40 + (0,5)N
N = 6k - 80
Σ Fy = 0 ==> N = 30 + 4k
Reemplazando el valor de N:
6k – 80 = 30 + 4k
2k = 110
K = 55
Pero:
F = 5k = (5)(55)
F = 55 N
|
Los hombres aprenden mientras enseñan.
SÉNECA, Lucio Anneo

