Un ejercicio sobre geometría analítica que nos ha llegado y nos parece interesante es el siguiente, espero que sea de utilidad para todos.
Hallar la ecuación de la circunferencia tangente a las rectas
L1 : x - 2y + 4 = 0;
L2 : 2x – y – 8 = 0
y que pase por el punto A(4,1).
Para resolver los ejercicios donde intervienen circunferencias se debe conocer su centro y su radio.
Para encontrar esta información utilizaremos las distancias desde el centro de la circunferencia a los puntos o rectas que nos dan como dato.
Sea C(h,k) el centro de la circunferencia y r su radio.
A(4,1)
L1 : x - 2y + 4 = 0
L2 : 2x – y – 8 = 0
Grafiquemos los datos que nos dan:

Entonces:
r = |d(C, L1)| = |d(C, L2)| = |d(A,C)|
Trabajamos primero con la siguiente igualdad:
|d(C, L1)| = |d(C, L2)|
Cálculo de la distancia de una recta a un punto dado:
Sí L : Ax + By + C = 0
y P(h,k)
El valor de la distancia no dirigida de dicha recta hasta el punto está dada por:

Reemplazando datos:
|h – 2k + 4| = |2h – k – 8|
De aquí:
h – 2k + 4 = 2h – k – 8 ==> k = 12 – h ………………I
o
h – 2k + 4 = - 2h + k + 8 ==> k = (3h – 4)/3 ………II
Ahora utilizaremos la ecuación del punto:
|d(C, L1)| = |d(A,C)|
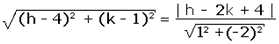
De donde:
5[(h – 4)2 + (k – 1)2] = (h – 2k + 4)2
5(h2 – 8h + 16 + k2 – 2k + 1) = h2 + 4k2 – 4hk + 8h – 16k + 16
5h2 – 40h + 80 + 5k2 – 10k + 5 = h2 + 4k2 – 4hk + 8h – 16k + 16
4h2 + k2 + 4hk – 48h + 6k + 69 =0 ……………………………………..III
Reemplazando I en III se obtiene:
4h2 + k2 + 4hk – 48h + 6k + 69 =0
4h2 + (12 – h)2 + 4h(12 – h) – 48h + 6(12 – h) + 69 =0
4h2 + 144 – 24h + h2 + 48h – 4h2 – 48h + 72 – 6h + 69 = 0
h2 – 30h + 285 = 0
Luego: (I) Ç (III) = ф
Reemplazando II en III se obtiene:
4h2 + k2 + 4hk – 48h + 6k + 69 =0
4h2 + [(3h - 4)/3]2 + 4h[(3h - 4)/3] – 48h + 6[(3h - 4)/3] + 69 =0
36h2 + 9h2 – 24h + 16 + 36h2 – 48h – 432h + 54 h – 72 + 621 =0
81h2 – 450h + 565 = 0
Resolviendo obtenemos:
h1 = 1.917
h2 = 3.638
y
k = (3h - 4)/3
k1 = 0.584
k2 = 2.305
Luego los centros de las circunferencias que cumplen con las condiciones de nuestro ejercicio son:
C1 (1.917, 0.584)
Y
C2 (3.638, 2.305)
Y sus respectivos radios serán:
r1 = |1.917 – 2(0.584) + 4 |/2.236
r1 = 2.124
r2 = |3.638 – 2(2.305) + 4 |/2.236
r2 = 1.354
Por lo tanto, las ecuaciones de las dos circunferencias buscadas son:
CIRCULO 1 : (x – 1.917)2 + (y – 0.584)2 = (2.124)2
CIRCULO 2 : (x – 3.638)2 + (y – 2.305)2 = (1.354)2
El gráfico de nuestra solución sería el siguiente:

Sigan enviando sus consultas a nuestro e-mail: jwzq2005@gmail.com
Si ayudo a una sola persona a tener esperanza, no habré vivido en vano.
KING, Martin Luther

