El siguiente ejercicio es una aplicación sobre matrices, espero que sea interesante para ustedes.

Recordemos que para multiplicar matrices se cumple que:

Emplearemos esta fórmula para ir deduciendo la matriz An.
Primero hallaremos A2

Ahora hallaremos A3

Por inducción matemática hallamos la matriz An

Para hallar la inversa utilizaremos el método de Gauss:
Sea A una matriz cuadrada de orden 3. Para calcular la matriz inversa de A, que denotaremos como A-1, seguiremos los siguientes pasos:
1º Construir una matriz del tipo M = (A | I), es decir, la matriz A está en la mitad izquierda de M y la matriz identidad I en la derecha.

2º Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A-1. Es decir, construiremos una matriz del tipo M = (I | A-1)
3º Se deja tal y como está la primera fila de M, y debajo del primer término de la diagonal principal, a11, que llamaremos pivote, realizamos operaciones para que se conviertan en ceros.


Ahora tomamos como pivote a22 y realizamos las operaciones para que se transforme en 1.

5º A continuación realizamos las operaciones necesarias en la fila 3 para que el término a32 sea cero

6º Finalmente la tercera fila se multiplica por n para que se convierta en 1.
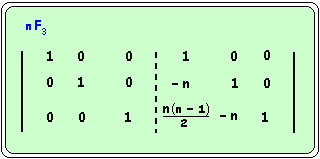
Con esto hemos logrado construir una matriz del tipo M = (I | A-1) y en consecuencia nuestra matriz solución es:

Sigan enviando sus consultas a nuestro e-mail jwzq2005@gmail.com
La suerte favorece sólo a la mente preparada.
ASIMOV, Isaac

